➡ Click here: Chi square table
The corresponding probability is between the 0. A cell χ 2 value less than 1. It enters all problems via its role in the , which is the distribution of the ratio of two independent chi-squared , each divided by their respective degrees of freedom.
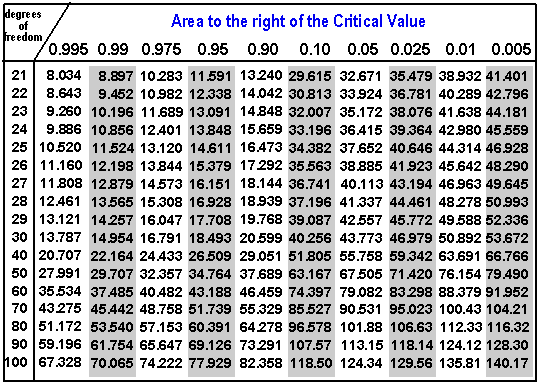
Therefore, this cell has a much larger number of servile cases than would be expected by chance. A probability is a number expressing the chances that a specific event will occur. The first and most commonly used is the Chi-square. No other cell has a cell χ 2 value greater than 0. It arises in the following north tests, among others. The company wanted to know if providing the vaccine made a difference. Following are some of the most common situations in which the chi-squared distribution arises from a Gaussian-distributed sample. Using a chi square table 2 table, the significance of a Chi-square value of 12. The medico reports that the cumulative probability is 0. They kept track of the number of employees who contracted pneumonia and which type of pneumonia each had.
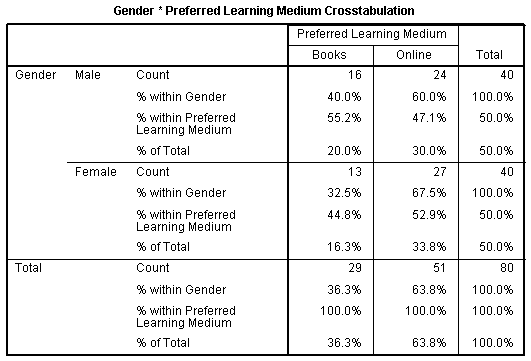
The second step is to calculate the expected values for each cell. Therefore, there is a 49% chance that the sample standard deviation will be no more than 0. The Symmetric Measures Table.
Chi-square table - Until the end of 19th century, Pearson noticed the existence of significant within some biological observations.

This article is about the mathematics of the chi-squared distribution. For its uses in statistics, see. For the music group, see. In and , the chi-squared distribution also chi-square or χ 2-distribution with k is the distribution of a sum of the squares of k random variables. The chi-square distribution is a special case of the and is one of the most widely used in , notably in or in construction of. When it is being distinguished from the more general , this distribution is sometimes called the central chi-squared distribution. Many other statistical tests also use this distribution, such as. The chi-squared distribution is used primarily in hypothesis testing. Unlike more widely known distributions such as the and the , the chi-squared distribution is not as often applied in the direct modeling of natural phenomena. It arises in the following hypothesis tests, among others. The primary reason that the chi-squared distribution is used extensively in hypothesis testing is its relationship to the normal distribution. Many hypothesis tests use a test statistic, such as the in a t-test. For these hypothesis tests, as the sample size, n, increases, the of the test statistic approaches the normal distribution. Because the test statistic such as t is asymptotically normally distributed, provided the sample size is sufficiently large, the distribution used for hypothesis testing may be approximated by a normal distribution. Testing hypotheses using a normal distribution is well understood and relatively easy. The simplest chi-squared distribution is the square of a standard normal distribution. So wherever a normal distribution could be used for a hypothesis test, a chi-squared distribution could be used. A sample drawn at random from Z is a sample from the distribution shown in the graph of the standard. Define a new random variable Q. To generate a random sample from Q, take a sample from Z and square the value. } The subscript 1 indicates that this particular chi-squared distribution is constructed from only 1 standard normal distribution. A chi-squared distribution constructed by squaring a single standard normal distribution is said to have 1 degree of freedom. Thus, as the sample size for a hypothesis test increases, the distribution of the test statistic approaches a normal distribution, and the distribution of the square of the test statistic approaches a chi-squared distribution. Just as extreme values of the normal distribution have low probability and give small p-values , extreme values of the chi-squared distribution have low probability. An additional reason that the chi-squared distribution is widely used is that it is a member of the class of LRT. LRT's have several desirable properties; in particular, LRT's commonly provide the highest power to reject the null hypothesis. However, the normal and chi-squared approximations are only valid asymptotically. For this reason, it is preferable to use the t distribution rather than the normal approximation or the chi-squared approximation for small sample size. Similarly, in analyses of contingency tables, the chi-squared approximation will be poor for small sample size, and it is preferable to use. Ramsey shows that the exact is always more powerful than the normal approximation. Lancaster shows the connections among the binomial, normal, and chi-squared distributions, as follows. De Moivre and Laplace established that a binomial distribution could be approximated by a normal distribution. In the case of a binomial outcome flipping a coin , the binomial distribution may be approximated by a normal distribution for sufficiently large n. Because the square of a standard normal distribution is the chi-squared distribution with one degree of freedom, the probability of a result such as 1 heads in 10 trials can be approximated either by the normal or the chi-squared distribution. However, many problems involve more than the two possible outcomes of a binomial, and instead require 3 or more categories, which leads to the multinomial distribution. Just as de Moivre and Laplace sought for and found the normal approximation to the binomial, Pearson sought for and found a multivariate normal approximation to the multinomial distribution. Pearson showed that the chi-squared distribution, the sum of multiple normal distributions, was such an approximation to the multinomial distribution Further properties of the chi-squared distribution can be found in the box at the upper right corner of this article. For derivations of the pdf in the cases of one, two and k degrees of freedom, see. Tables of the chi-squared cumulative distribution function are widely available and the function is included in many and all. } For another for the CDF modeled after the cube of a Gaussian, see. Additivity It follows from the definition of the chi-squared distribution that the sum of independent chi-squared variables is also chi-squared distributed. Since the chi-squared is in the family of gamma distributions, this can be derived by substituting appropriate values in the. For derivation from more basic principles, see the derivation in. The sampling distribution of ln χ 2 converges to normality much faster than the sampling distribution of χ 2, as the logarithm removes much of the asymmetry. Other functions of the chi-squared distribution converge more rapidly to a normal distribution. } This is known as the Wilson—Hilferty transformation. Difference between numerical quantile and approximate formula bottom. The sum of squares of unit-variance Gaussian variables which do not have mean zero yields a generalization of the chi-squared distribution called the. } The chi-squared distribution is also naturally related to other distributions arising from the Gaussian. If X 1 and X 2 are not independent, then X 1 + X 2 is not chi-squared distributed. The chi-squared distribution is obtained as the sum of the squares of k independent, zero-mean, unit-variance Gaussian random variables. Generalizations of this distribution can be obtained by summing the squares of other types of Gaussian random variables. Several such distributions are described below. It may be, however, calculated using the of the chi-squared random variable. The chi-squared distribution has numerous applications in inferential , for instance in and in estimating. It enters the problem of estimating the mean of a normally distributed population and the problem of estimating the slope of a line via its role in. It enters all problems via its role in the , which is the distribution of the ratio of two independent chi-squared , each divided by their respective degrees of freedom. Following are some of the most common situations in which the chi-squared distribution arises from a Gaussian-distributed sample. The is the probability of observing a test statistic at least as extreme in a chi-squared distribution. Accordingly, since the CDF for the appropriate degrees of freedom df gives the probability of having obtained a value less extreme than this point, subtracting the CDF value from 1 gives the p-value. A low p-value, below the chosen significance level, indicates , i. A significance level of 0. The table below gives a number of p-values matching to χ 2 for the first 10 degrees of freedom. Degrees of freedom df χ 2 value 1 0. This distribution was first described by the German statistician in papers of 1875—6, where he computed the sampling distribution of the sample variance of a normal population. The distribution was independently rediscovered by the English mathematician in the context of , for which he developed his , published in 1900, with computed table of values published in , collected in , pp. John Willey and Sons. Introduction to the Theory of Statistics Third ed. Understanding Advanced Statistical Methods. Boca Raton, FL: CRC Press. Journal of Educational Statistics. Random Structures and Algorithms. Simon, Probability Distributions Involving Gaussian Random Variables, New York: Springer, 2002, eq. Supplement to the Journal of the Royal Statistical Society. Journal of the Royal Statistical Society. McLaughlin at The Pennsylvania State University. In turn citing: R. Yates, Statistical Tables for Biological Agricultural and Medical Research, 6th ed. Two values have been corrected, 7. Sampling Distributions under Normality. Plackett, Karl Pearson and the Chi-Squared Test, International Statistical Review, 1983, See also Jeff Miller,.

